This is the first part of a two-part blog post about PlumX and Wikipedia mentions. In this first one, we explore the meaning and possible interpretations of Wikipedia mentions of scholarly output, both on an individual piece of research and when aggregated. In the second, we will discuss the alternative ways to calculate such a metric. (The second is about calculating Wikipedia mentions.)

A Wikipedia Mention is when a research artifact is literally mentioned in a Wikipedia article. This could be anywhere in the body of the article text, or in the references section. Wikipedia mentions are an important altmetric for understanding both societal impact and the context in which a work is being understood and talked about.

The size and reach of the world’s most exhaustive online encyclopedia are undeniable. Launched in 2001, Wikipedia grew quickly and includes over 5.2 million English articles, over 40M total wiki pages, and over 20,000 new articles added monthly. References to any research on this platform are highly visible; the English version of Wikipedia alone has over 7 billion page views per month.

A 3:AM Conference blog post from August 2016 highlighted two open questions about Wikipedia mentions:

• What does a Wikipedia mention mean? What conclusions can be drawn from looking at this metric?
• What is the best way to calculate a mention metric?

In the first of two blog posts about Plum Analytics and Wikipedia, we will tackle the first question.

There is a distinction between how Wikipedia mentions can be interpreted when looking at an individual piece of research vs. when looking at the total count of such references for a group of scholarly outputs.

Wikipedia Mentions of a Research Output: It’s All About Context

The 3:AM Conference blog post clearly highlights that interpreting the impact of any single Wikipedia mention of a particular research output can be a challenge. We’ve certainly found this within the research that we track at Plum Analytics. A Wikipedia post mentioning a piece of research could be a post about a broad topic referencing an important book about the topic. On the other hand, it could simply be a Wikipedia page for one of the researchers involved, referencing the output in a list of publications. To understand the underlying story, easy access to the context is key.

In the following example, this book is referenced only once in Wikipedia – but in a post about a broad topic.

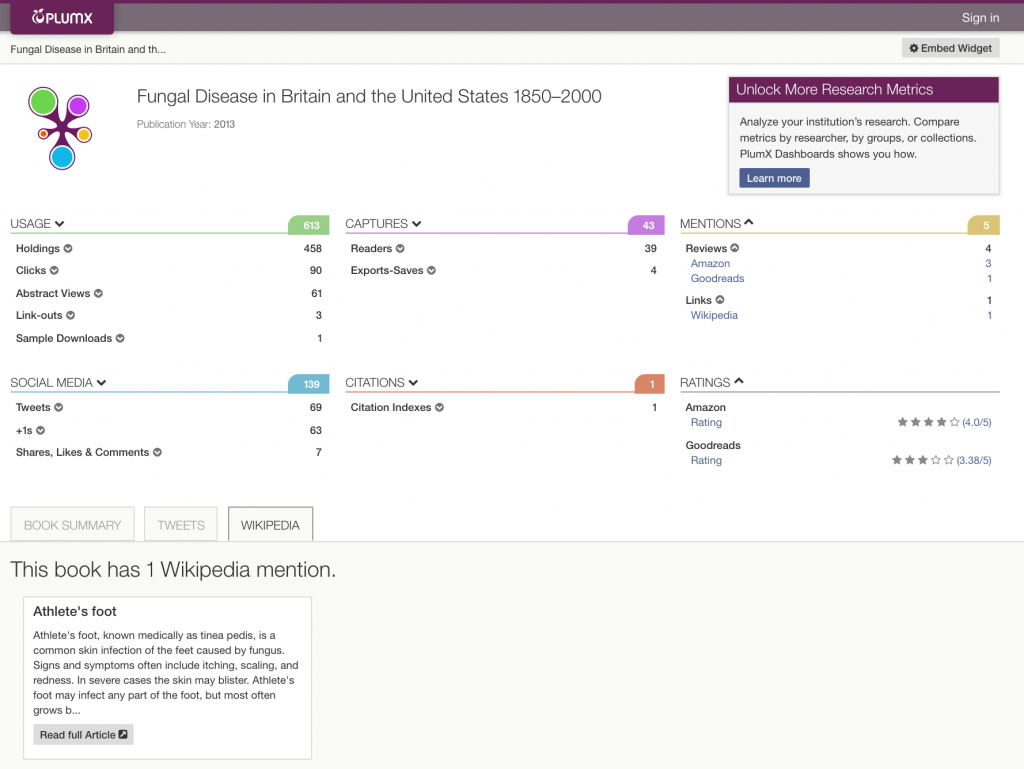
Note that as often is the case for books, citations fail to tell a compelling story about this work. The library holdings information, book ratings and reviews from Amazon and Goodreads, and Wikipedia mentions in a post about a very broad topic show that this work carries some weight as an authoritative source.

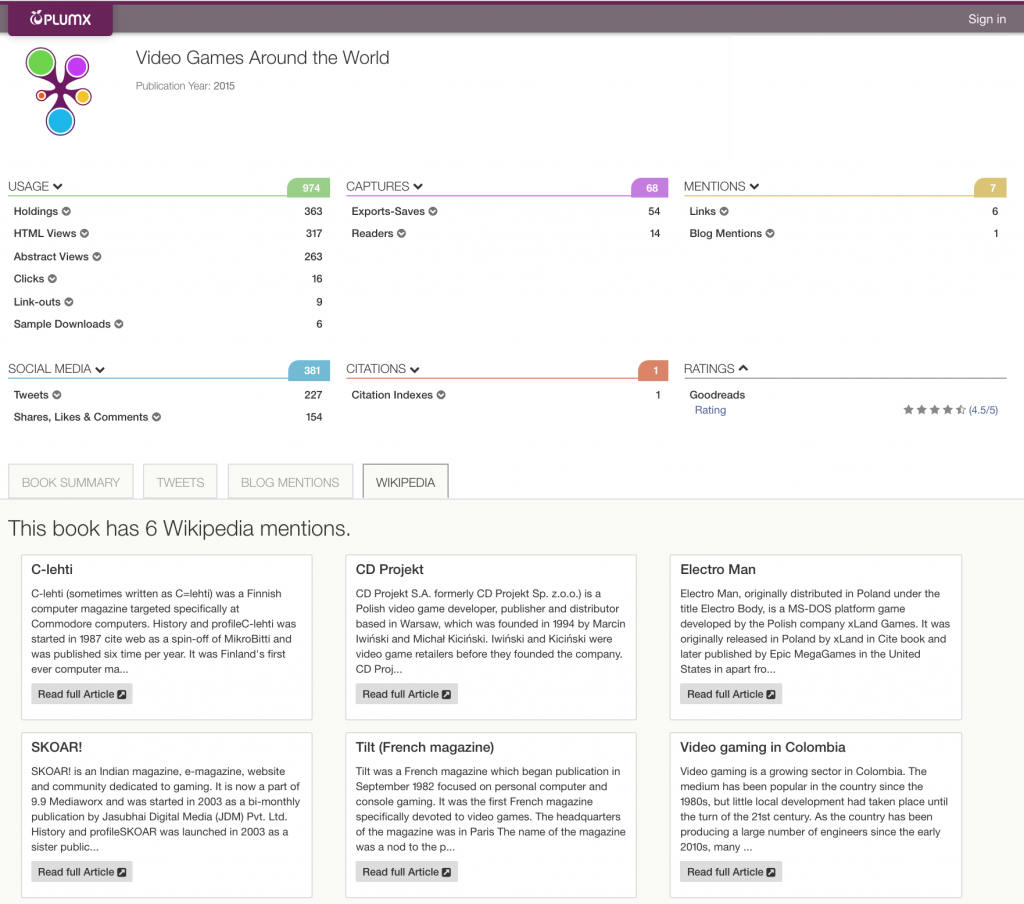
Another book showcases the how the broadness of the topics in referring Wikipedia posts varies – from a post about 1992 Polish video game “ElectroMan” (narrow) to video gaming in Columbia (much broader).

Clearly, to tell the story of how a piece of research is being used and discussed, understanding this type of context for a Wikipedia mention is important.

When looking at an individual research output, the PlumX Wikipedia tab displays all mentions listed alphabetically by post title. Each Wikipedia mention ‘card’ displays the post title, a snippet of the post and a link to the original post. This helps you quickly see at a glance the kinds of Wikipedia content that are linking to a work, and explore the page, the context of the reference and even the page history in more depth if needed.

Aggregating Wikipedia Mentions

A PlumX artifact page tells the story for an individual piece of research. But could you also use these metrics to answer questions about sets of research and how they compare? Is it useful to compare counts of Wikipedia mentions aggregated by researcher, department, or grant?

Aggregated Wikipedia mentions are a useful tool for academic administrators looking for trends, patterns and anomalies in how a group of research is being used or where it is gaining attention. When a researcher, department or grant shows more Wikipedia engagement than their peers, explore deeper in PlumX and Wikipedia to find out:

• Is this engagement concentrated on one or just a few pieces of research? Or are mentions evenly distributed across a larger body of work? Is a particular researcher or subject area showing higher levels of engagement?
• Is this engagement something you want to replicate? How does Wikipedia engagement vary between your experienced researchers and your rising stars? Does a path to success in certain subject areas often involve popular engagement with the research?
• When were references added? Do they reflect renewed popular interest in a particular paper (see Sleeping Beauty Papers) or a subject area?

As is the case with so many altmetrics measures, the counts assigned to a paper, researcher or school aren’t nearly as important as the stories these patterns and analyses allow you to uncover about the research.

A common pitfall is attempting to interpret a count of Wikipedia mentions as a measure of quality or impact, that is, trying to use this number to ‘score’ researchers or departments. This notion is especially dangerous when reward systems are tied to such scores, because the underlying meaning can be so variable. Another reason treating counts of wikipedia mentions as comparison scores can be problematic is that you need to be sure that all of your researchers’ outputs are accounted for. Before undertaking any aggregated analysis of a group of researchers, ensuring all research is adequately represented and tracked equally is key for a valid comparison.

Clearly to make these kinds of decisions, the underlying data must be robust and as complete as possible. The mechanisms you use to calculate the metric are also key. In part 2 of this blog post we’ll dive into the alternative strategies.